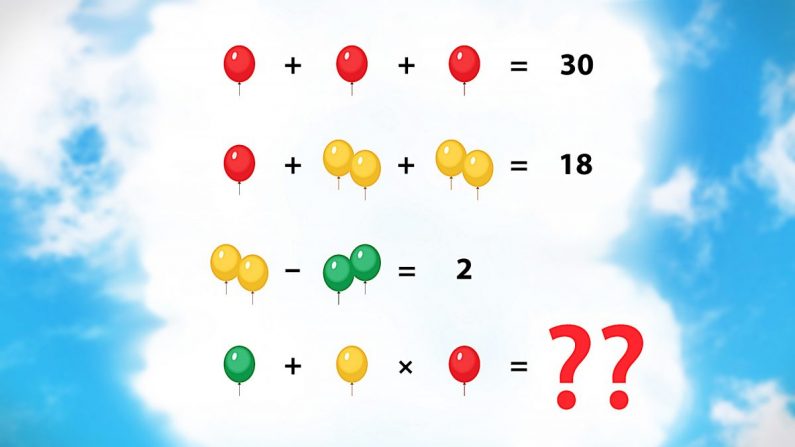Nous ne sommes pas nombreux à pouvoir résister à un bon défi cérébral – ajoutez quelques ballons à l’équation, et vous êtes accro ! Celui-ci est devenu viral et a circulé sur Internet récemment, et il a même suscité l’intérêt de quelques docteurs en mathématiques.
Jetez un coup d’œil au problème de mathématiques des ballons ci-dessous, et à l’aide des équations données, voyez si vous pouvez résoudre la dernière question.
Pouvez-vous trouver la réponse ?

Prenez un moment ou deux pour faire le point dans votre tête ou sur papier – ce sera une bonne occasion de prendre une pause bien méritée dans votre travail acharné et de vous recentrer avec des mathématiques avant de commencer votre journée.
Lorsque vous pensez avoir trouvé la solution, vous trouverez ci-dessous une explication et la réponse finale.

Tout d’abord, nous allons décomposer le problème ligne par ligne et résoudre chaque partie de l’équation. Cela devrait nous permettre de résoudre l’équation finale.
Dans la première équation, nous avons 1 ballon rouge plus 1 ballon rouge plus 1 ballon rouge, ce qui équivaut à 30. Cela signifie que chaque ballon rouge est égal à 10.

Dans la deuxième équation, nous voyons qu’un ballon rouge plus deux ballons jaunes plus deux ballons jaunes égalent 18. Puisque nous avons établi qu’un ballon rouge est égal à 10, nous pouvons le soustraire des deux côtés de l’équation, et nous savons maintenant que 2 ballons jaunes plus 2 ballons jaunes sont égaux à 8. Par conséquent, 2 ballons jaunes correspondent à 4.

Troisièmement, nous avons 2 ballons jaunes moins 2 ballons verts, ce qui équivaut à 2. Parce que nous savons maintenant que 2 ballons jaunes valent 4, nous pouvons maintenant déterminer que 2 ballons verts valent 2.
Maintenant, nous avons la valeur de tous les ballons, et nous sommes donc en mesure de résoudre la dernière équation.

Ainsi, nous pouvons résoudre la quatrième équation, 1 ballon vert plus 1 ballon rouge multiplié par 1 ballon jaune.
Les trois premières équations nous ont appris que 2 ballons jaunes égalent 4, et 2 ballons verts égalent 2. Il semble donc raisonnable qu’un ballon jaune soit égal à 2, et qu’un ballon vert soit égal à 1.

De plus, vous devez vous rappeler qu’il existe un ordre d’opérations pour résoudre l’addition et la multiplication ; les multiplications doivent être résolues en premier, sinon la réponse sera incorrecte.
Dix multiplié par 2 égale 20, plus 1 égale 21. La réponse est 21.
Avez-vous réussi à résoudre ce problème de mathématiques ? Avouez-le, ce sont les ballons qui ont retenu votre attention, n’est-ce pas ? Néanmoins, vous avez probablement trouvé la résolution de ce puzzle au moins un peu satisfaisante. C’est parce que votre cerveau adore assembler des puzzles et résoudre des problèmes – ainsi que la satisfaction de pouvoir s’en vanter par la suite.
*Si vous vous demandez pourquoi ce puzzle susciterait l’intérêt des docteurs en mathématiques, regardez cette vidéo (elle vous rendra probablement fou avec son jargon mathématique sophistiqué)
BONUS : Êtes-vous prêt à relever un défi encore plus difficile ? Essayez celui-ci !

Pouvez-vous résoudre la séquence ? Il y a deux solutions (mais vous aurez besoin d’un QI de 130+ pour la deuxième)
Maintenant, certains d’entre vous, sceptiques, regardent peut-être ce casse-tête et pensent : « La réponse est 19. Cela ne fait aucune différence que deux des équations précédentes soient fausses. » Et en ce qui nous concerne, vous avez raison de penser cela ! Si vous déclarez que 19 est votre réponse, nous la prenons. C’est sortir des sentiers battus !
Mais pour ceux qui veulent vraiment tester leur mental, ce casse-tête a encore quelques tours dans sa manche, comme vous le verrez.

Il y a quelques formules cachées dans la séquence d’équations qui relient tout cela pour vous donner la vraie réponse. Mais vous devrez trouver la formule pour pouvoir résoudre cette séquence. Êtes-vous prêt à le faire ?
Regardons encore une fois :

Prenez un moment pour examiner les modèles à l’œuvre. Conseil : il existe deux solutions possibles (outre la réponse 19 mentionnée ci-dessus). Essayez de trouver les deux solutions avant de faire défiler les réponses ci-dessous.
VOYEZ LA RÉPONSE CI-DESSOUS
Solution 1 :
La première équation est tout à fait logique : 1 + 4 = 5, naturellement. Mais c’est là que la logique semble s’arrêter. Les deuxième et troisième équations, 2 + 5 = 12 et 3 + 6 = 21, ne sont pas équivalentes, à moins qu’il n’y ait une explication plus large ou une règle cachée qui ne nous est pas donnée dans la séquence. Si nous pouvons déterminer ce que c’est, nous pourrons peut-être résoudre la dernière équation.
Le modèle :
Ajoutez le côté gauche de toute équation donnée à la réponse de l’équation précédente (selon l’illustration ci-dessous). Dans le cas de la première équation, il n’y a pas d’équation précédente, et vous ajouteriez donc zéro au côté gauche de l’équation (0 + 1 + 4), ce qui vous donne 5. Le même schéma fonctionne pour les deuxième et troisième équations, et nous savons donc qu’il est correct. Appliquez cette règle à la dernière équation, et nous obtenons la solution.

La réponse pour la solution 1 est donc 40.
En suivant ce schéma, nous pouvons résoudre l’équation finale en ajoutant la réponse précédente (21) au côté gauche de ladite équation (8 + 11), ce qui nous donne 40.
Solution 2 :
Vous avez peut-être pensé que c’est tout ce qu’il y a à faire, mais en fait, comme certains d’entre vous l’ont peut-être remarqué, il y a un autre modèle caché dans la séquence, et cela donne une deuxième solution qui fonctionne également. Elle utilise le premier modèle, mais donne une réponse différente, mais parfaitement valable.
Le deuxième modèle :
Observez comment le premier nombre de chacune des trois premières équations crée une séquence consécutive : 1, 2, 3 ; et comment le deuxième nombre de chacune des trois premières équations crée une autre séquence consécutive : 4, 5, 6.
La dernière équation peut sembler rompre ce schéma consécutif, mais en fait, elle s’inscrit dans la séquence si vous admettez que des parties de cette séquence existent mais sont omises de la vue, comme le montre l’illustration ci-dessous :

Et puisque la séquence entière a maintenant changé – y compris l’avant-dernière équation en particulier – et en supposant que nous utilisions la même règle que la solution 1 pour résoudre la dernière équation, nous obtiendrons une réponse différente, comme vous pouvez le voir sur l’illustration ci-dessous :

Et la réponse pour la solution 2 est 96 !
Comment pouvez-vous nous aider à vous tenir informés ?
Epoch Times est un média libre et indépendant, ne recevant aucune aide publique et n’appartenant à aucun parti politique ou groupe financier. Depuis notre création, nous faisons face à des attaques déloyales pour faire taire nos informations portant notamment sur les questions de droits de l'homme en Chine. C'est pourquoi, nous comptons sur votre soutien pour défendre notre journalisme indépendant et pour continuer, grâce à vous, à faire connaître la vérité.